机器学习基本要素

机器学习的三要素：模型、学习准则、优化。

模型

线性模型：$f(x,\theta)=\textbf{w}^T\textbf{x}+b$
非线性模型：广义的非线性模型可以写为多个非线性基函数𝜙(𝒙) 的线性组合。$f(x,\theta)=\textbf{w}^T\phi(\textbf{x})+b$ 如果 $\phi(\textbf{x})$本身为可学习的基函数，则$f(x,\theta)$就等价于神经网络模型

学习准则

模型的好坏可以通过期望风险衡量； 损失函数是非负实数函数，常见的损失函数：

  1. 0-1损失：不连续且导数为 0，难以优化
  2. 平方损失：一般不适用于分类问题。$y$为实数值 $$\mathcal{L}(y, f(\mathbf{x};\theta))=\frac{1}{2}\left(y-f(\mathbf{x};\theta))\right)^2$$
  3. 交叉熵：一般用于分类问题 $\mathbf{y}$为one-hot标签向量 $$ \begin{align} \mathcal{L}(\mathbf{y}, f(\mathbf{x};\theta))&=-\mathbf{y}\mathrm{log}f(\mathbf{x};\theta) \\ &= - \sum^{C}_{c=1}y_c\mathrm{log}f_c(\mathbf{x};\theta) \\ &= -\mathrm{log}f_y(\mathbf{x};\theta) \end{align} $$

因此，交叉熵损失函数也就是负对数似然函数。

经验风险最小化(Empirical Risk Minimization，ERM)原则：找到一组参数使得经验风险最小。

过拟合

在训练集上错误率很低，但是在未知数据上错误率很高.往往是由于训练数据少和噪声以及模型能力强等原因造成的

为了解决过拟合问题， 一般在经验风险最小化的基础上再引入参数的正则化 (Regularization)来限制模型能力，使其不要过度地最小化经验风险。这种准则就是结构风险最小化(Structure Risk Minimization，SRM)准则 $$ \theta^*=\underset{\theta}{\arg \min } \frac{1}{N} \sum_{n=1}^N \mathcal{L}\left(y^{(n)}, f\left(\boldsymbol{x}^{(n)} ; \theta\right)\right)+\lambda \mathscr{l}_p(\theta) $$ 最大似然估计

最大后验估计

所有损害优化的方法都是正则化，包括增加优化约束、干扰优化过程（提前停止、随机梯度下降） $\mathscr{l}_2$范数正则化项，各个参数的平方和的开方值，用来减少参数空间，避免过拟合; $\lambda$用来控制正则化的强度。
$\mathscr{l}_1$范数正则化项，各个参数的绝对值之和，通常会使得参数有一定稀疏性。

加入正则化后，参数被限制到了一定的区域，等价于下面带约束条件的优化问题， $$ \begin{aligned} & \theta^*=\underset{\theta}{\arg \min } \frac{1}{N} \sum_{n=1}^N \mathcal{L}\left(y^{(n)}, f\left(\boldsymbol{x}^{(n)} ; \theta\right)\right), \\ & \text { s.t. } \quad \ell_p(\theta) \leq d \end{aligned} $$ $\mathcal{F}$为函数$f(\theta)$的等高线(为简单起见，这里用直线表示)。可以看出，$\mathscr{l}_1$范数的约束通常会使得最优解位于坐标轴上，意味着某一维会变为0，从而使得最终的参数为稀疏性向量。 $\mathscr{l}_2$参数取值空间是圆形，比较平滑，很难与损失函数的曲线相交在顶点上，但是它会使得参数更接近与0。

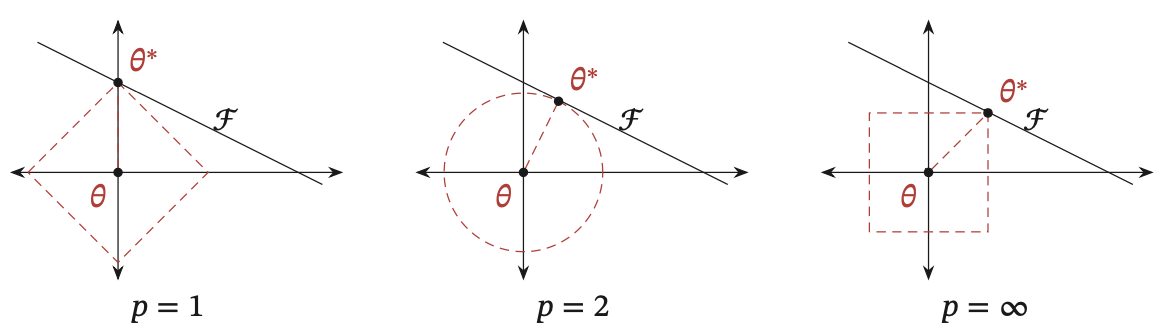
不同范数约束条件下的最优化问题示例

不同范数约束条件下的最优化问题示例

$\mathscr{l}_2$范数约束条件下的最优化问题示例

$\mathscr{l}_2$范数约束条件下的最优化问题示例

$\mathscr{l}_1$范数约束条件下的最优化问题示例

$\mathscr{l}_1$范数约束条件下的最优化问题示例

从贝叶斯学习的角度来讲，正则化是引入了参数的先验分布，使其不完全依赖训练数据1。

优化

参数是模型的参数 超参数是定义模型结构或优化策略的参数，e.g. learning rate

针对梯度下降的优化算法，除了加正则化项之外，还可以通过提前停止来防止过拟合。如果在验证集上的错误率不再下降，就停止迭代。

梯度下降

批量梯度下降法(Batch Gradient Descent，BGD)在每次迭代时需要计算每个样本上损失函数的梯度并求和。

在每次迭代时只采集一个样本，计算这个样本损失函数的梯度并更新参数，即随机梯度下降法(Stochastic Gradient Descent，SGD)

随机梯度下降实现简单，收敛速度也非常快，因此使用非常广泛。随机梯度下降相当于在批量梯度 下降的梯度上引入了随机噪声，在非凸优化问题中，随机梯度下降更容易逃离局部最优点。

小批量梯度下降法(Mini-Batch Gradient Descent)是批量梯度下降和随机梯度下 降的折中.每次迭代时，我们随机选取一小部分训练样本来计算梯度并更新参数，这样既可以兼顾随机梯度下降法的优点，也可以提高训练效率

批量大小的影响

批量大小不影响随机梯度的期望，但是会影响随机梯度的方差。
批量越大，随机梯度的方差越小，引入的噪声也越小，训练也越稳定，因此可以设置较大的学习率。
而批量较小时，需要设置较小的学习率，否则模型会不收敛。

小批量梯度下降中，每次选取样本数量对损失下降的影响

小批量梯度下降中，每次选取样本数量对损失下降的影响

  • 从(a)可以看出，每次迭代选取的批量样本数越多，下降效果越明显，并且曲线越平滑。当每次选取一个样本时（相当于随机梯度下降），损失整体是下降趋势，但局部看会来回震荡。
  • 从(b)可以看出，如果按整个数据集迭代的来看损失变化情况，则小批量样本数越小，下降效果越明显。

线性回归

  1. TODO ↩︎